Находим производные: f'(x)=3x^2-1, g'(x)=6x-4.
Значение производной в точке касания определяет угловой коэффициент касательной в этой точке. Поскольку касательные параллельны, то производные можно приравнять (у касательных равны угловые коэффициенты), поэтому 3x^2-1=6x-4<=>3x^2-6x+3=0<=>x^2-2x+1=0=>
=>x1=1,x2=1. f(1)=1^3-1-1=-1, g(1)=3*1^2-4*1+1=0. f'(1)=2, g'(1)=2.
Составляем уравнения касательных: f(x)=>y+1=2(x-1), y=2x-3,
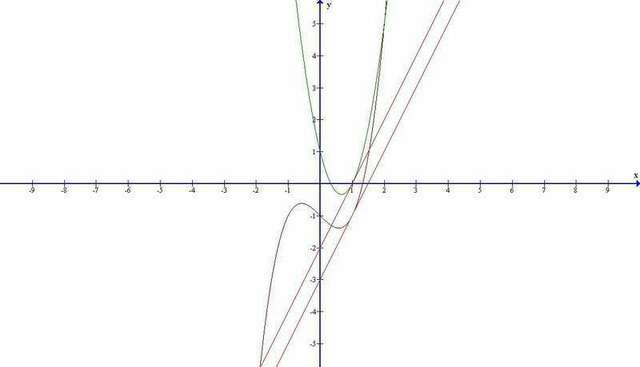
g(x)=>y-0=2(x-1), y=2x-2. Ну, и для наглядности графики