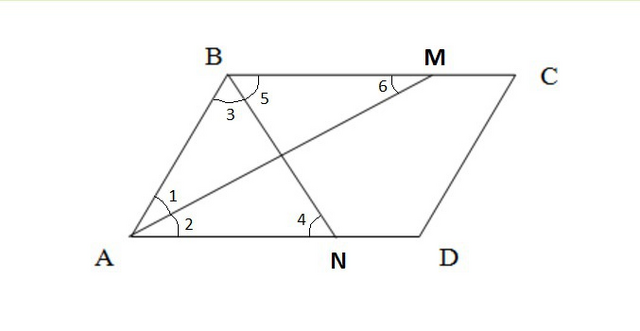
Из свойств биссектрисы параллелограмма: биссектриса угла параллелограмма отсекает от него равнобедренный треугольник. Отсюда ΔABN и ΔАВМ - равнобедренные.
В ΔABN ∠BAN=∠BNA.
∠4=∠5 как накрестлежащие при ВС║AD и секущей BN.
∠5=∠3 так как BN биссектриса ⇒ ∠3=∠4 ⇒ ΔABN - равносторонний ⇒ AN=AB=8м
Так как ΔABM равнобедренный, то АВ=ВМ=8м
ВС=ВМ+МС=8+3=11м
P=2(AB+BC)=2(8+11)=2*19=38м
Ответ: 38 м.