Пожалуйта помогите решить! Круг, центр которого принадлежит стороне AВ треугольника ABC ,...

Question

Пожалуйта помогите решить!

Круг, центр которого принадлежит стороне AВ треугольника ABC , проходит через точку В , прикасается к стороне АС в точке С и пересекает сторону АВ в точке D. Найти углы треугольника АВС, если AD:DB=1:2.

Answer 1

Решение в приложенном рисунке.

Answer 2

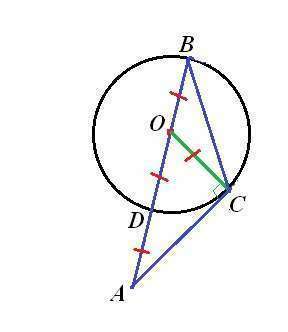
Чертеж во вложении.
Т.к. АД:ДВ=1:2, и ДВ-диаметр, то АД=ДО=ОВ=ОС.
∆ АОС - прямоугольный, гипотенуза АО в 2 раза больше катета ОС, значит, в нем ∠А=30°, и ∠АОС=60°.
∆ ВОС - равнобедренный, значит, в нем ∠В=∠ВСО=60°/2=30°.
Теперь ∠ВСА=90°+30°=120°.
Итак в ∆ АВС ∠А=30°, ∠В=30°, ∠С=120°.

---