Основы равнобедренной трапеции 15 и 33 см,а диагональ делит ее острый угол напополам ....

Question

Основы равнобедренной трапеции 15 и 33 см,а диагональ делит ее острый угол напополам . Найти площадь трапеции :?
Если есть возможность , можно решение с рисунком )

Answer 1

 AD - большее основание
 /_А острый угол . /_CAD=/_ACB  (накрест лежащие углы )
/_ ACB=/_CAB=> ABC равнобедренный AB=BC=15.
BH-высота трапеции
AH=(33-15)/2=9
BH=VAB^2-AB^2=12
S= (AD+BC)*BH/2=(15+33)*12/2=288 

Comments

ad /_А острый угол . /_CAD=/_ACB (накрест лежащие углы )/_ ACB=/_CAB=> ABC равнобедренный AB=BC=15.BH-высота трапецииAH=(33-15)/2=9BH=VAB^2-AB^2=12S= (AD+BC)*BH/2=(15+33)*12/2=288

Answer 2

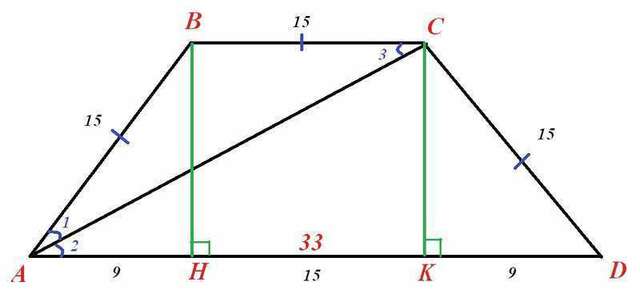
Чертежик во вложении.
Т.к. диагональ АС - биссектриса угла А, то ∠1=∠2.
Отсюда ∠2=∠3 (накрестлежащие).
Значит, ∠1=∠3 и ∆АВС-равнобедренный с основанием АС, тогда АВ=ВС=15 см.
Проведем высоты ВН и СК. Т.к. HBCK-прямоугольник, то ВС=НК.
Прямоугольные треугольники АВН и СДК равны по гипотенузе и катету, значит, у них АН=КД=(33-15)/2=9 см.
В прямоугольном ∆АВН по теореме Пифагора 

Ответ: 288 см2.

---