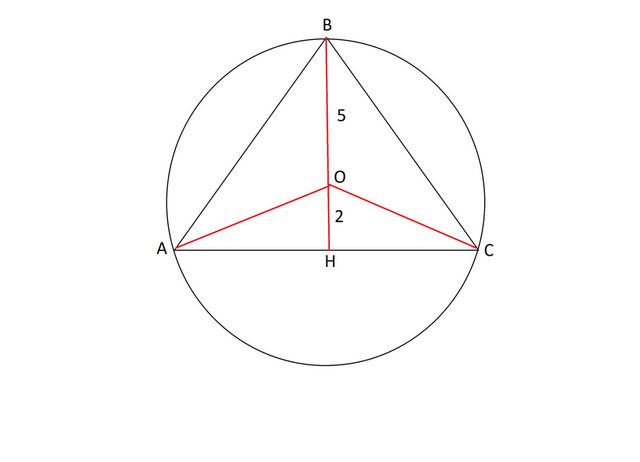
Cделаем и рассмотрим рисунок.
Центр окружности лежит на высоте. Вершины треугольника лежат на окружности.
Следовательно, отрезок от вершины В до цетнра О - радиус окружности.
Он равен 5.
Соединим центр с любой из других вершин углов треугольника, т.к.он равнобедренный и выбор не влияет на решение.
Получим прямоугольный треугольник АОН, в котором АН, половина основания треугольника, и отрезок ОН - катеты, а ОА - (радиус окружности) - гипотенуза.
По т.Пифагора найдем АН -половину основания АС.
АН²=АО²-ОН²
АН²=5²-2²=21
АН=√21
Площадь треугольника равна половине произведения основания на высоту.
Высота равна 5+2=7см
S=7√21cм²
Но:
----------------------------------------------------
Возможно, в условии задачи ошибкаи высота центром делится не на 5 и 2, а на 5 см и 4 см
Тогда
АН²=5²-4²=9
АН=3
S=7*3=21 cм²