Найдём точки пересечения(общая точка) графиков приравняя функции.

Графики имеют 1 точку пересечения, когда дискриминант x^2-x(3+k)+4 будет равен нулю.

В точках k=-7;k=1 графики будут иметь ровно одну точку пересечения. Т.к. k у нас только при положительных k, то k=1.
Коордінаты точки: 

Координата точки:(2;-2)
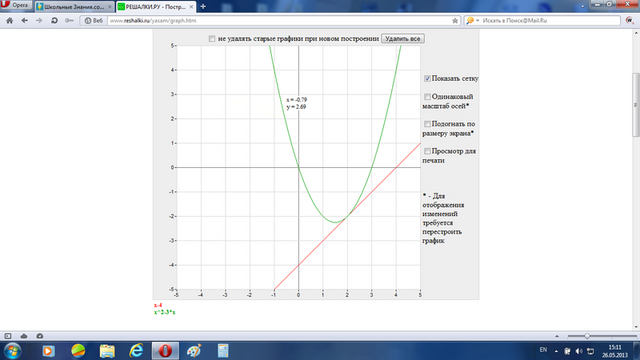
График во вложении.