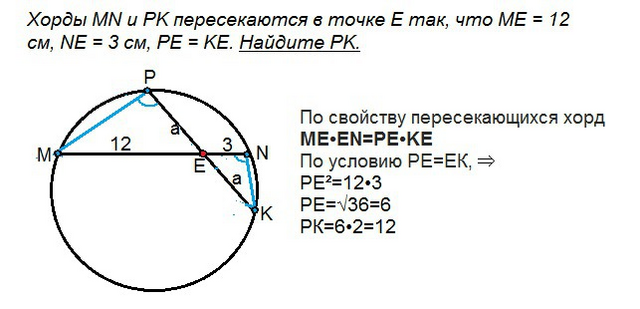
Даны две пересекающиеся хорды. Длины отрезков хорды MN равны 12 и 3. Пусть длины каждого из отрезков второй хорды будут а, т.к. они по условию равны.
Углы с вершинами Р и N вписанные и опираются на одну и ту же дугу. Все вписанные углы, опирающиеся на одну и ту же дугу равны. ⇒ ∠ MPК =∠МNK .
Соединим отрезками точки М и Р и точки K и N
В треугольниках MPЕ и ЕNK углы при Е равны как вертикальные, ∠ MPЕ =∠ЕNK . ⇒
∆ MPЕ ~∆ ЕNK по первому признаку подобия треугольников.
Из подобия следует отношение сходственных сторон:
МЕ:КЕ=РЕ:ЕN ⇒
ME•EN=KE•PE
12•3=а²
а=√36=6
РК=6•2=12 см
________________
Данный способ решения применён при доказательстве теоремы:
Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды.
Её применение сделает запись решения короче:
По свойству пересекающихся хорд
МЕ•EN=PE•KE
По условию РЕ=ЕК, ⇒
РЕ²=12•3
РЕ=√36=6
РК=6•2=12 см