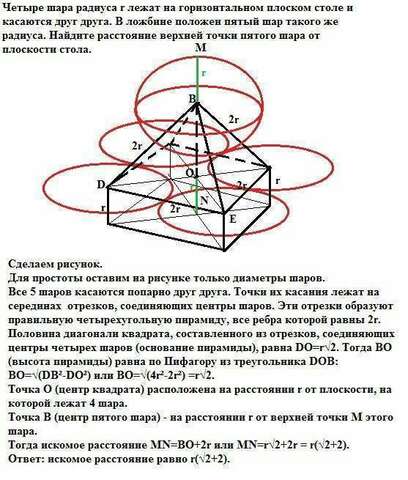
Сделаем рисунок.
Для простоты оставим на рисунке только диаметры шаров.
Все 5 шаров касаются попарно друг друга. Точки их касания лежат на
серединах отрезков, соединяющих центры шаров. Эти отрезки образуют правильную четырехугольную пирамиду, все ребра которой равны 2r.
Половина диагонали квадрата, составленного из отрезков, соединяющих центры
четырех шаров (основание пирамиды), равна DO=r√2. Тогда ВО (высота пирамиды) равна по Пифагору из треугольника DOB:
ВО=√(DB²-DO²) или ВО=√(4r²-2r²) =r√2.
Точка О (центр квадрата) расположена на расстоянии r от плоскости, на которой
лежат 4 шара. Точка В (центр пятого шара) - на расстоянии r от верхней точки М этого шара. Тогда искомое расстояние MN=BO+2r или MN=r√2+2r = r(√2+2).
Ответ: искомое расстояние равно r(√2+2).