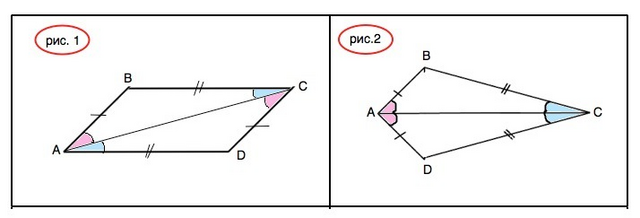
По условию диагональ АС делит четырехугольник на два равных треугольника.
а)
Пусть АВ=CD. (см. рис. 1)
Из равенства треугольников следует равенство их сходственных элементов.
Тогда:
Угол ВСА=САD, ВАС=АСD. Эти углы - накрестлежащие при пересечении прямых секущей. Если накрестлежащие углы при пересечении двух прямых секущей равны - эти прямые параллельны.
Следовательно, BC II AD и AB II CD.
б)
То же самое можно доказать из равенства противолежащих сторон треугольников.
АВ=CD, BC=AD, АС - общая.
Если противолежащие стороны четырехугольника попарно равны, этот четырехугольник - параллелограмм. По определению противолежащие стороны параллелограмма параллельны.
Следовательно, BC II AD и AB II CD
———
Условие задачи некорректное - не указана пара равные сторон. Иначе доказательство параллельности противоположных сторон может оказаться невозможным. Диагональ АС делит четырёхугольник на два равных треугольника (см. признаки равенства треугольников), но противолежащие стороны не параллельны. (См. рис.2)