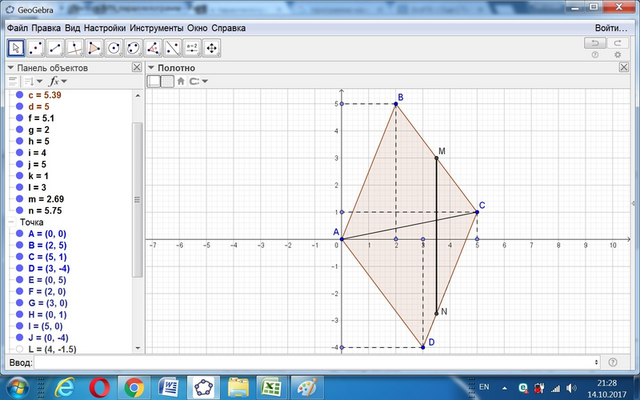
Дан параллелограмм ABCD. AB (2;5), AD (3;-4) ,точки M и N лежат на сторонах BC и CD соответственно так ,что BM=MC, CN:ND=3:1.
Расположим параллелограмм точкой А в начало координат.
Точка А(0; 0).
Тогда координаты точек В и D равны координатам векторов AB и D:
B (2;5), D (3;-4).
Вектор АС равен сумме векторов AB и AD:
АС = (2+3=5; 5-4=1) = (5; 1).
Координаты точки С тоже равны (5; 1).
Находим координаты точки М как середину вектора ВС:
М=((2+5)/2=3,5; (5+1)/2=3) = (3,5; 3).
Координаты точки N находим по формуле деления отрезка CD.
Деление отрезка СD
в
данном отношении 3/1:

xN = (5+3*3)/(1+3) = 14/4 = 3,5.
yN = (1+3*(-4))/(1+3) =-11/4 = -2,75.
а) Координаты вектора MN:
MN = ((3,5-3,5=0; -2,75-3=-5,75) = (0; -5,75).
б) Разложение вектора MN по координатный векторам i и j:
(0i; -5,75j).
в) Длина вектора AC = √(0² + (-5,75)²) = 5,75.