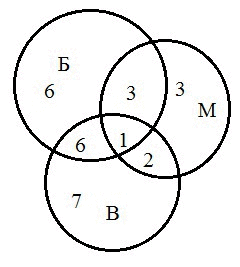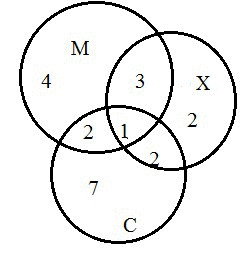3) Решение: В этой задаче 3 множества, из условий задачи видно, что все они пересекаются между собой. Только "Белоснежку" выбрали 16-6-3-1=6 человек. Только "Микки-Маус" выбрали 9-3-2-1=3 человека.
Только "Винни-Пух" выбрали 28-(6+3+3+2+6+1)=7 человек. Тогда, учитывая, что некоторые выбрали по несколько мультфильмов, получаем, что "Винни-Пух" выбрали 7+6+1+2=16 человек.
4) Решение: В этой задаче 3 множества, из условий задачи видно, что все они пересекаются между собой. Только музыкальную школу посещают 10-3-2-1=4 учащихся. Только художественную школу посещают 8-3-2-1=2 учащихся. Только спортивную школу посещают 12-2-2-1=7 учащихся.
Только одну школу посещают 4+2+7=13 учеников.
Ни в чем себя не развивают 24-(4+2+7+3+2+2+1)=3 учащихся.
Ответ. 13 учеников посещают только одну школу, 3 учащихся себя не развивают.
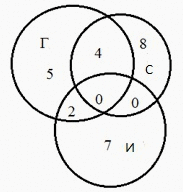
5) Решение: Так как Гриша всего проиграл в 11 игр, из них 4 головоломки решены Сашей и 2 головоломки - Игорем, то 11 - 4 - 2 = 5 - игр проиграно только Гришей. Следовательно, 26 - 7 - 2 - 5 - 4 = 8 - головоломок решено только Сашей. А всего Саша играл в игр.
Ответ. 12 игр решил Саша.