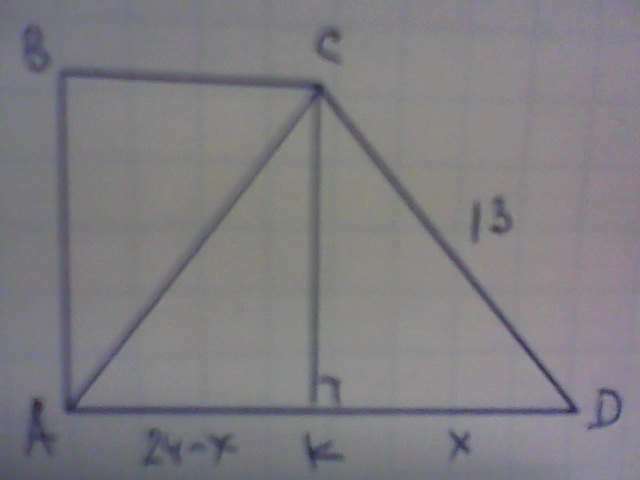
Дано: АВСD- прямоугольная трапеция, АВ⊥АD, АD=24 см, СD=13 см, АС-меньшая диагональ трапеции. СD=АС=13 см.
Найти периметр АВСD.
Решение.
Проведем СК⊥АD, АВСК=прямоугольник, СК=АВ.
Пусть DК=х, АК=24-х.
ΔСDК. СК²=СD²-CК²=13²-х².
ΔВСК. СК²=АС²-АК²=13²-(24-х)².
13²-х²=13²-(24-х)²,
-х²=-(24-х)²,
х²=576-48х+х²,
48х=576,
х=576/48=12.
СК=12 см.
ΔСDК. СК²=СD²-DК²; DК²=13²-12²=169-144=25; DК=√25=5 см.
АК=24-5=19 см АК=ВС= 19 см.
Найдем периметр Р= 12+19+13+24=68 см.
Ответ: 68 см.