|x + 1| – |x| + 3|x – 1| – 2|x – 2| = x + 2;
Уравнение можно решить методом интервалов.
Находим нули модулей: -1; 0; 1; 2.
Нули модулей разбивают числовую прямую на промежутки:
(-∞;-1), [-1;0), [0;1), [1;2), [2;+∞).
Определяем знаки модулей на этих промежутках (это удобно делать в таблице):
(-∞;-1), [-1;0), [0;1), [1;2), [2;+∞).
x+1 - + + + +
x - - + + +
x-1 - - - + +
x-2 - - - - +
Раскрываем модули,согласно таблице, и смотрим,чтобы полученное решение соответствовало промежутку:
(-∞;-1):-x-1+x-3x+32x-4-x-2=0; x=-2 ∈ (-∞;-1) - подходит;
[-1;0): x+1+x-3x+3+2x-4-x-2=0; 0≠2 - нет решений;
[0;1): x+1-x-3x+3+2x-4-x-2=0; x=-1 ∉ [0;1) - не подходит;
[1;2): x+1-x+3x-3+2x-4-x-2=0; x=-2 ∉ [1;2) - не подходит;
[2;+∞): x+1-x+3x-3-2x+4-x-2=0; 0=0 - это значит, что значение х=2 является решением уравнения.
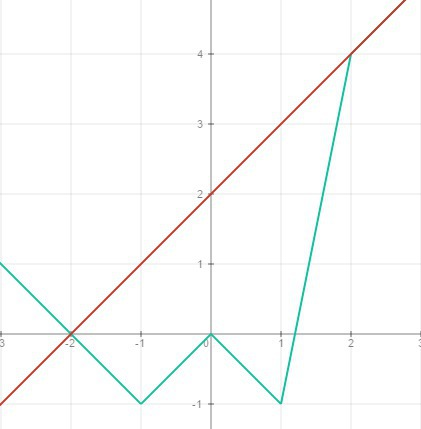
Таким образом, получаем два решения х=-2 и х=2.
Это хорошо видно на графике.
Ответ: -2; 2.