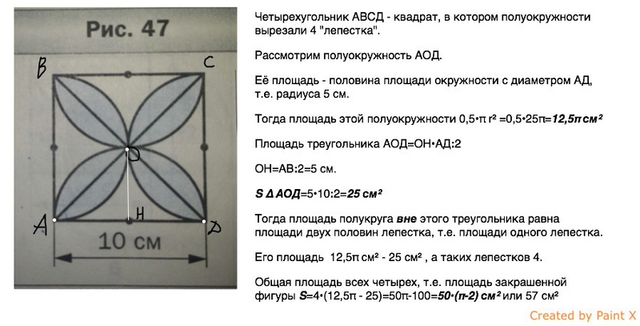
Четырехугольник АВСД - квадрат, в котором полуокружности вырезали 4 "лепестка".
Рассмотрим полуокружность АОД.
Её площадь - половина площади окружности с диаметром АД, т.е. радиуса 5 см.
Тогда площадь этой полуокружности 0,5•π r² =0,5•25π=12,5π см²
Площадь треугольника АОД=ОН•АД:2
ОН=АВ:2=5 см.
S ∆ АОД=5•10:2=25 см²
Тогда площадь полукруга вне этого треугольника равна площади двух половин лепестка, т.е. площади одного лепестка.
Его площадь 12,5π см² - 25 см² , а таких лепестков 4.
Общая площадь всех четырех, т.е. площадь закрашенной фигуры
S=4•(12,5π - 25)=50π-100=50•(π-2) см² или 57 см²