Найдём нули функции:
Так как в знаменателе

то область определения функции (-∞;1) ∪ (1;∞)
Дробь равна нулю только если числитель равен нулю, а знаменатель при этом не равен нулю.
получаем уравнение

Из этого имеем 2 линейных уравнения и квадратичное


больше нуля всегда
Остается:

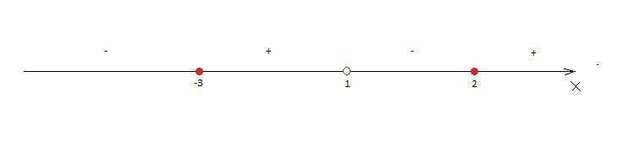
Имеем три координаты -3;1;2 (рисунок прилагаю) и соответственно 4 интервала.
Нас интересуют только те интервалы где функция меньше либо равна нулю. 1 не включается, т.к. функция в данной точке не существует
Ответ: x∈(-∞;-3] ∪ (1;2]