ДАНО
Y = 2x³+3x²-5
ИССЛЕДОВАНИЕ
1. Область определения - существования - все R или
Х∈(-∞,+∞) и вывод - разрывов нет.
2. Пересечение с осью абсцисс - ось Х .
X = -1. - без комментариев.
3. Пересечение с осью ординат - ось У
У(0) = 5.
4. Поведение на бесконечности
У(-∞) = - ∞ и У(+∞) = +∞.
5. Исследование на чётность
У(-х) = -2х³+3х²-5
У(+х) = 2х³+3х² -5
У(х) ≠ У(-х) - функция ни чётная ни нечётная.
6. Поиск экстремумов по производной функции.
У'(x) = 6*x²+6х = 6*х(x+1)
Нули производной - х1 = 0, х2 = -1.
7. Монотонность
Возрастает - Х∈(-∞,-1]∪[0,+∞) - вне корней производной.
Убывает - Х∈[-1,0] - внутри корней производной.
8. Значение в точках экстремума
Ymax(-1) = -4
Ymin(0) = -5
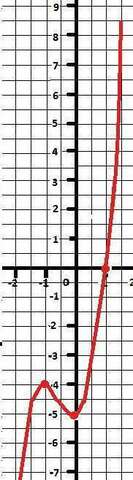
9. Построение графика.
Вычисляем дополнительные точки.
Y(-2) = -9
Y(1.5) = 8.5
И готово - в приложении.