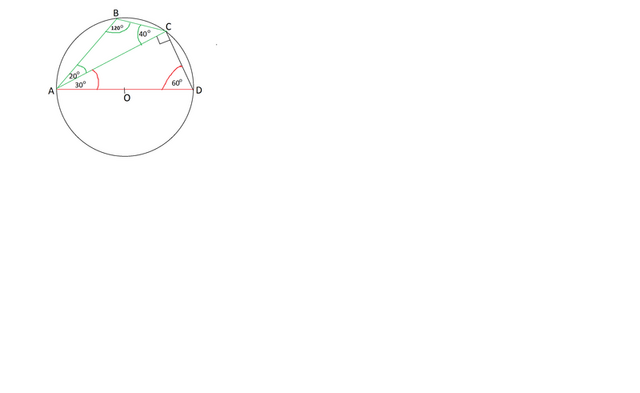
Сделаем рисунок.
Обозначим вершины треугольника А, В, С.
Диаметр пусть будет АD.
Сума углов треугольника 180°ВАС+ВСА=20°+40°=60°.
Угол АВС=180°-60°=120°.
Так как углы треугольника вписанные,
угол АВС опирается на дугу 120°*2=240°.
Соединим С и D
Расмотрим треугольник АСD
Посколькоу дуга АDC, на которую опирается угол АВС, равна 240°,
дуга АВС равна 360°-240°=120°, а вписанный угол СDА,опирающийся на нее, равен половине градусной меры этой дуги и равен 120°:2=60°.
Так как гол АСD опирается на диаметр АD, треугольник АСD - прямоугольный.
Отсюда угол САD=30°.
АС, большая сторона треугольника АВС, противолежит углу 60°
АС=АD*sin(60°)=(10*√3):2=5√3
--------------------------------------
Вариант решения:
Угол АВС=180-20-40=120 градусов.
Рассмотрим четырехугольник АВСD. Он вписанный в окружность.
Сумма противоположных углов вписанного четырехугольника равна 180 градусов.
Следовательно, угол АDC равен
180-120=60 градусов.
Так как угол АСD опирается на диаметр, треугольник АСD - прямоугольный.
АС, большая сторона треугольника АВС, противолежит углу 60°
АС=АD*sin(60°)=(10*√3):2=5√3