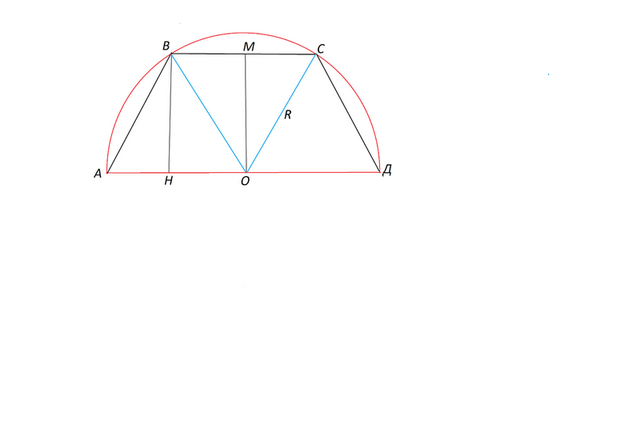
В полукруг единичного радиуса вписана трапеция так, что ее основание лежит на диаметре. Найти площадь трапеции, если ее периметр равен 5.
Большее основание АД равно диаметру и равно 2.
Пусть меньшее основание ВС равно х.
Тогда боковая сторона АВ равна половине разности между периметром и суммой оснований.
АВ=(5- 2-х):2=(3-х):2
Найдем высоту Н=МО=ВН из двух прямоугольных треугольников и приравняем значения:
1) Н=МО из ОМС
Н²=R²- МС²=1-(х:2)²=(4-х²):4
2)Н=ВН из АНВ
Высота трапеции, опущенная на большее основание, делит его на отрезки, меньший из которых равен полуразности оснований.
АН=(АД-ВС):2=(2-х):2
Н²=АВ²- АН²= {(3-х):2}² - {(2-х):2}²=(5-2х):4
(4-х²):4=(5-2х):4
Получим квадратное уравнение:
х²-2х+1=0
Дискриминант равен нулю, уравнение имеет один корень.
х=1
Подставим найденное значение в
Н²=R²- МС²=1-0,25=0,75
Н=0,5√ 3
S=[(2+1):2]*0,5√3=1,5*0,5√3=0,75√3 или ≈1,3