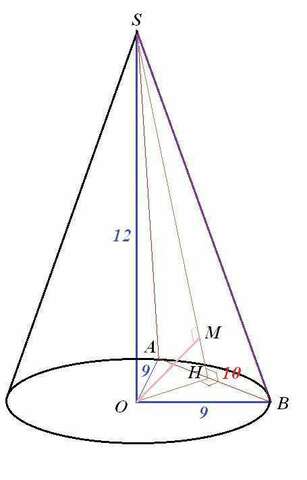
Чертеж к задаче во вложении.
Хорда в основании конуса - отрезок АВ=10.
Плоскость, проходящая через вершину конуса и хорду АВ, это ∆ASB.
Расстояние от О до этого ∆ - это отрезок ОМ. Его и надо найти.
1) ∆АОВ-равнобедренный (ОА=ОВ=9). ОН- мединана, бссектриса, высота ∆АОВ.
АН=ВН=5.
2) По теореме Пифагора в ∆ВОН

3) По теореме о трех перпендикулярах прямая АВ, проведенная на плоскости через основание Н наклонной SH, перпендикулярна ее проекции ОН, значит АВ перпендикулярна наклонной SH. Тогда в силу того что Н - середина АВ имеем, что SH - и медиана и высота ∆ASB. Т.е. этот треугольник равнобедренный и у него SA=SB.
4) По теореме Пифагора в ∆SОН

5) Рассмотрим прямоугольный ∆SOH. Пусть НМ = х, тогда SM = 10√2 - х
По теореме Пифагора в ∆МОН

По теореме Пифагора в ∆МОS

Получаем уравнение:

Ответ: