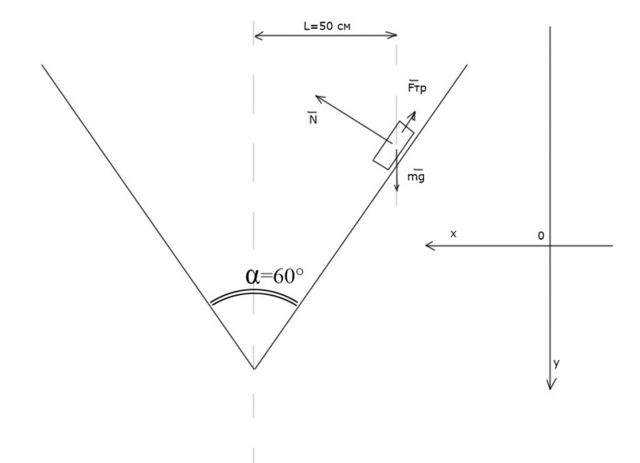
Найдём условие равновесия:
Для этого, по вертикали должен быть нулевой баланс сил:
Ny + Fтрy + mg = 0 ;
mg = Nsin(α/2) + Fтр cos(α/2) ;
Отсюда: Nsin(α/2) = mg – Fтр cos(α/2) ; [1] ;
и одновременно: Fтр cos(α/2) = mg – Nsin(α/2) ; [2]
Баланс сил по горизонтали должен обеспечивать центростремительное ускорение, направленное к оси:
( Nx + Fтрx ) / m = a(n) = Lω² ;
( Ncos(α/2) – Fтр sin(α/2) ) / m = Lω² ;
Отсюда: Ncos(α/2) = mLω² + Fтр sin(α/2) ; [3] ;
и одновременно: Fтр sin(α/2) = Ncos(α/2) – mLω² ; [4]
Поделим уравнения [4] и [2] и получим:
tg(α/2) = ( Ncos(α/2) – mLω² ) / ( mg – Nsin(α/2) ) ;
mg tg(α/2) – Nsin(α/2)tg(α/2) = Ncos(α/2) – mLω² ;
N ( sin(α/2)tg(α/2) + cos(α/2) ) = mg tg(α/2) + mLω² ;
N = m ( g tg(α/2) + Lω² ) / ( sin(α/2)tg(α/2) + cos(α/2) ) ;
Поделим уравнения [1] и [3] и получим:
tg(α/2) = ( mg – Fтр cos(α/2) ) / ( mLω² + Fтр sin(α/2) ) ;
mLω²tg(α/2) + Fтр sin(α/2) tg(α/2) = mg – Fтр cos(α/2) ;
Fтр ( sin(α/2) tg(α/2) + cos(α/2) ) = m( g – Lω²tg(α/2) ) ;
Fтр = m( g – Lω²tg(α/2) ) / ( sin(α/2) tg(α/2) + cos(α/2) ) ;
Для силы трения в покое существует незыблемое условие:
|Fтр| < μN, иначе система выйдет из равновесия:
| ( g – Lω²tg(α/2) ) / ( sin(α/2) tg(α/2) + cos(α/2) ) | < μ ( g tg(α/2) + Lω² ) / ( sin(α/2)tg(α/2) + cos(α/2) ) ;
| g – Lω²tg(α/2) | < μ ( g tg(α/2) + Lω² ) ;
– μ ( g tg(α/2) + Lω² ) < g – Lω²tg(α/2) < μ ( g tg(α/2) + Lω² ) ; [5]
Решаем левое условие [5]:
– μg tg(α/2) – μLω² < g – Lω²tg(α/2) ;
μg tg(α/2) + g > Lω²tg(α/2) – μLω² ;
g ( μtg(α/2) + 1 ) > ω²L( tg(α/2) – μ ) ;
что верно всегда, поскольку последняя скобка tg(α/2) – μ = 1/√3 – 0.8 < 0 , а левая часть положительна.
Отсюда заключаем, что даже если сила трения при некоторых угловых скоростях и может развернуться, т.е. стать направленной вниз, против стремления бруска заползать наверх, то эта сила трения ни при каких угловых скоростей не выйдет за пределы силы трения скольжения, а стало быть никакой угловой скоростью, даже очень большой брусок не удастся поднять выше начального положения.
Решаем правое условие [5]:
g – Lω²tg(α/2) < μg tg(α/2) + μLω² ;
g ( 1 – μ tg(α/2) ) < Lω² ( tg(α/2) + μ ) ;
ω² > (g/L) ( 1 – μ tg(α/2) ) / ( tg(α/2) + μ ) ;
Отсюда заключаем, что что лишь выше определённой угловой скорости брусок будет оставатья в покое, а при проходе этого значения вниз, к меньшим угловым скоростям – брусок потеряет равновесие и станет скатываться.
При этом, любопытно, что чем на меньшем удалении от оси нам нужно удерживать брусок, тем большая (!) требуется угловая скорость (зависимость-то гиперболическая!), а у нас происходит напртив, не увеличение скорости, а её снижение. А значит, как только угловая скорость пройтёт вышеуказанное значение брусок окончательно потеряет равновесие и свалится в вершину конуса.
Искомая угловая скорость: ω = √[ (g/L) ( 1 – μ tg(α/2) ) / ( tg(α/2) + μ ) ] ;
ω = √[ (9.8/0.5) ( 1 – 0.8/√3 ) / ( √3 + 0.8 ) ] ≈ 2.77 / с ;
Ответ: 2.77 / с .