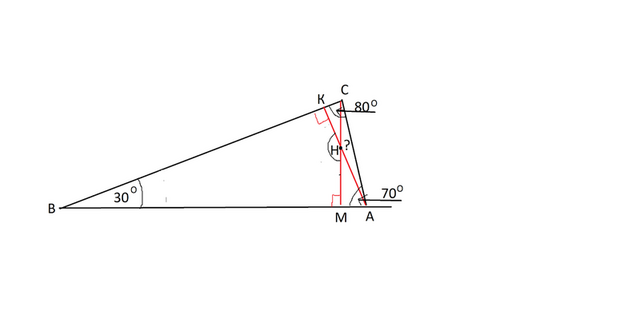
Сделаем по условию задачи рисунок и рассмотрим его.
В треугольнике АВС ∠А=70°, ∠С=80°.
Третий угол этого треугольника ∠С=180°-(80°+70°)=30°
Высоты из А и С образуют в точке пересечения с ВС и АС прямые углы.
В то же время точка пересечения этих высот Н - одна из вершин четырехугольника ВКНМ.
Сумма углов четырехугольника равна 360°.
Так как известны три угла четырехугольника ВКНМ, четвертый
∠КНМ= 360°- (∠КВМ+ ∠НМВ+∠НКВ)=150°
Искомый угол АНС равен КНМ как вертикальный.
Ответ: ∠АНС=150°