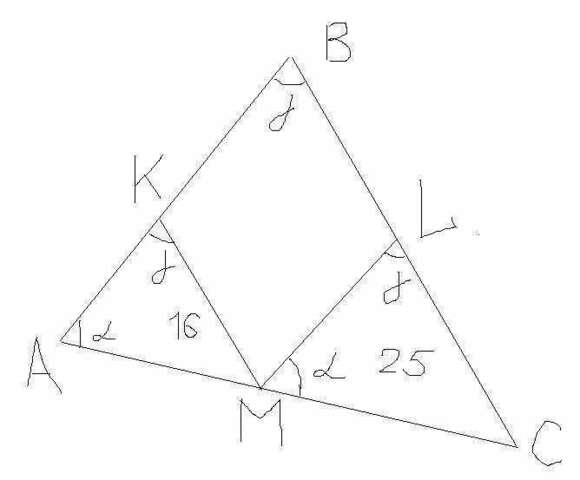
Дано: 
Найти: 
Решение: Заметим, что  по двум углам. Один угол общий,
по двум углам. Один угол общий,  - как односторонние углы при параллельных прямых КМ и ВС и секущей ВК.
- как односторонние углы при параллельных прямых КМ и ВС и секущей ВК.
Также  по двум углам. Один угол общий,
по двум углам. Один угол общий,  - как односторонние углы при параллельных прямых LМ и AВ и секущей ВC.
- как односторонние углы при параллельных прямых LМ и AВ и секущей ВC.
Значит, по свойствам подобия треугольников

Вычислим коэффициент подобия этих треугольников

Заметим также, что
 - по свойству параллельных прямых.
- по свойству параллельных прямых.
По свойству параллелограмма ML=KB. По свойству подобия треугольников

Пусть АК=4х, тогда КВ=ML=5x. AK+KB=AB=4x+5x=9x.
Значит  - это коэффициент подобия треугольников AKM и AВС. Вычислим площадь теугольника АВС.
- это коэффициент подобия треугольников AKM и AВС. Вычислим площадь теугольника АВС.

По своствам площадей

Подставим известные значения



Ответ: