Решить систему графическим способом (x+2y=3 < (-4x+y=6 ( <---------это птичка также...

Question

Решить систему графическим способом

(x+2y=3

<

(-4x+y=6

(

<---------это птичка также и вверху</p>

(

Answer 1

Графики данных функций - прямые. Зададим точки для этих прямых:

(1) - y=0 => x=3

        y=1,5 => x = 0

(2) - y=0 => x = -1,5

        y=6 => x = 0

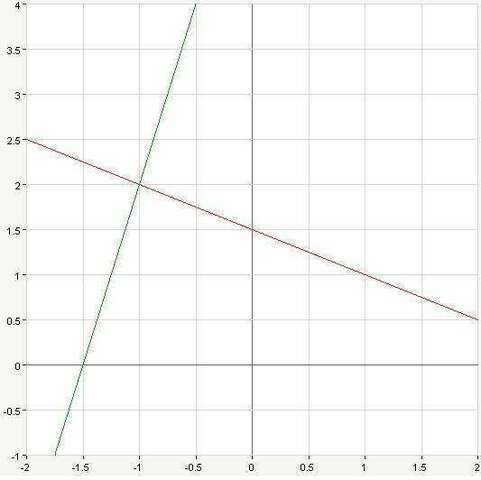
Начертим графики данных функций (см. влож).

По графику видно, что прямые пересекаются в точке (-1; 2).

Значит, решение системы x=-1, y=-2.

---