В цилиндр вписана призма. Основанием призмы служит прямоугольный треугольник, катет...

Question

Дано ответов: 2

Правильный ответ

Основанием вписанной в цилиндр призмы служит прямоугольный треугольник. Он вписан в круг - основание цилиндра.

Гипотенуза вписанного прямоугольного треугольника - диаметр окружности, в которую он вписан.
Диаметр АВ =ВС: cos( 30°)
АВ=2:(√3 : 2)=4:√3=4:√3
По условию диагональ большей боковой грани призмы составляет с плоскостью ее основания угол в 45°.
Большая боковая грань призмы имеет основанием большую сторону основания - гипотенузу АВ.
Отсюда высота АЕ цилиндра, как катет ЕА равнобедренного прямоугольного треугольника ЕАВ равна АВ и равна 4:√3
V=πr²H
r=0,5*4:√3 =2:√3
V=π(2:√3 )²(4:√3)=π4*4: 3√3=16π√3:3*3=16π√3):9

Hrisula_zn (228k баллов) 12 Март, 18

artalex74_zn · Answer 1 · 2018-03-12T03:01:42+0000

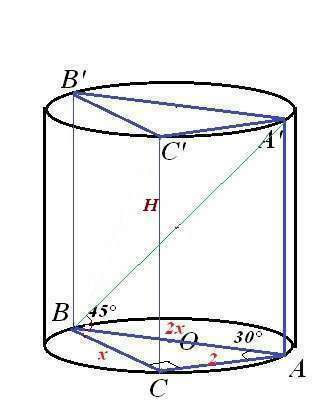
Чертеж к задаче во вложении.

∆ АВС - прямоугольный, ∠С=90°, ∠А=30°. Следовательно, гипотенуза АВ является диаметром описанной окружности (основания цилиндра) и АВ=2ВС. По теореме Пифагора

$AB^2=BC^2+AC^2 \\\ (2BC)^2=BC^2+2^2 \\\ BC^2=\frac{4}{3} \\\ BC=\frac{2\sqrt3}{3} \\\ AB=\frac{4\sqrt3}{3}$

Рассмотрим прямоугольный ∆ ВАА'. У него по условию ∠B=45°, следовательно ∠А'=90°-45°=45°. Поэтому ∆ ВАА' - равнобедренный с основанием BА'. Значит,

$AA'=AB=H=\frac{4\sqrt3}{3} \\\ V=\pi R^2H \\\ R=\frac{1}{2}AB=BC=\frac{2\sqrt3}{3} \\\ V=\pi (\frac{2\sqrt3}{3})^2*\frac{4\sqrt3}{3}=\frac{16\pi \sqrt3}{9}$