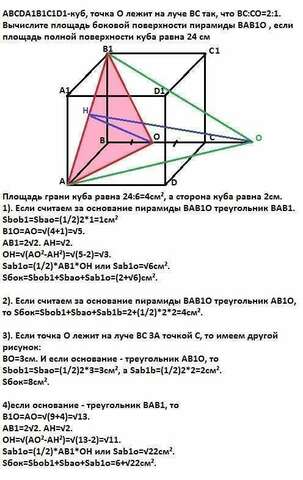
ABCDA1B1C1D1-куб, точка O лежит на луче BC так, что BC:CO=2:1. Вычислите
площадь боковой поверхности пирамиды BAB1O , если площадь полной поверхности
куба равна 24 см².
Площадь грани куба равна 24:6=4см², а сторона куба равна 2см.
1). Если считаем за основание пирамиды ВАВ1О треугольник ВАВ1.
Sbob1=Sbao=(1/2)2*1=1см²
В1О=АО=√(4+1)=√5.
АВ1=2√2. АН=√2.
ОН=√(АО²-АН²)=√(5-2)=√3.
Sab1o=(1/2)*АВ1*ОН или Sab1o=√6см².
Sбок=Sbob1+Sbao+Sab1o=(2+√6)см².
2). Если считаем за основание пирамиды ВАВ1О треугольник АВ1О,
то Sбок=Sbob1+Sbao+Sab1b=2+(1/2)*2*2=4см².
3). Если точка О лежит на луче ВС ЗА точкой С, то имеем другой рисунок:
ВО=3см. И если основание - треугольник АВ1О, то
Sbob1=Sbao=(1/2)2*3=3см², а Sab1b=(1/2)2*2=2см².
Sбок=8см².
4)если основание - треугольник ВАВ1, то
В1О=АО=√(9+4)=√13.
АВ1=2√2. АН=√2.
ОН=√(АО²-АН²)=√(13-2)=√11.
Sab1o=(1/2)*АВ1*ОН или Sab1o=√22см².
Sбок=Sbob1+Sbao+Sab1o=6+√22см².