οбласть : 
первая производная :

второя производная :

принципя
1. f(x) возрастающая если производная > 0
2. f(x) убывающая если производная < 0
3. f(x) неубывающая и невозрастающая (стала или екстремум ) если производная = 0
4. f(x) вypuкла если второя производная > 0
5. f(x) вогнутая если второя производная < 0
6. f(x) невypuкла и невогнутая ( перегиб или прямая ) если второя производная = 0
ад 3
екстрема




ад 1
возрастание
 0 \newline \newline \frac x 2(x -4) > 0" alt="\frac{x^2}{2}-2x > 0 \newline \newline \frac x 2(x -4) > 0" align="absmiddle" class="latex-formula">
0 \newline \newline \frac x 2(x -4) > 0" alt="\frac{x^2}{2}-2x > 0 \newline \newline \frac x 2(x -4) > 0" align="absmiddle" class="latex-formula">  4}} \right" alt="\left \{ {{x<0} \atop {x>4}} \right" align="absmiddle" class="latex-formula">
4}} \right" alt="\left \{ {{x<0} \atop {x>4}} \right" align="absmiddle" class="latex-formula">
ад 2
убывание


ad 6
перегиб


ad 4
выпукла:
 0 \newline \newline x >2" alt="x-2 > 0 \newline \newline x >2" align="absmiddle" class="latex-formula">
0 \newline \newline x >2" alt="x-2 > 0 \newline \newline x >2" align="absmiddle" class="latex-formula">
ад 5
вогнутая

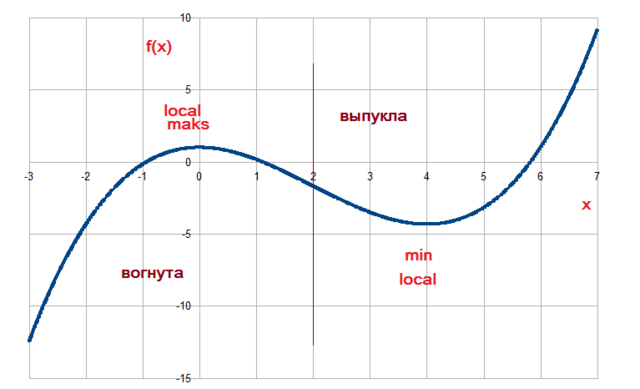
тепер рисуем : во вложению граф