Стороны паралелограма 4 и 5 см а диагональ соединющая вершини острых углов равна √61см....

0 голосов
196 просмотров

Стороны паралелограма 4 и 5 см а диагональ соединющая вершини острых углов равна √61см. Найти углы паралелограмма?

Только напишите пожалуйста полное решение

Геометрия (22 баллов) | 196 просмотров
Дан 1 ответ
0 голосов
Правильный ответ

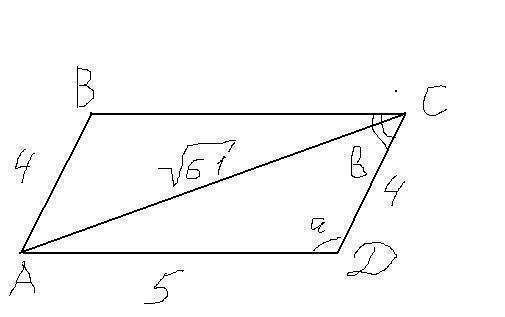
Теорема косинусов. Рассмотрим треугольник, образованный двумя сторонами параллелограмма и известной диагональю. По теореме косинусов обозначим угол между сторонами параллелограмма за а, тогда получаем следующую формулу

 

(\sqrt{61})^2=5^2+4^2-2*5*4*\cos a

 

61=25+16-40*\cos a

 

61=41-40*\cos a

 

61-41=-40*\cos a

 

20=-40*\cos a

 

0,5=-\cos a

 

cos a = -0,5

 

a=120^0

 

Другой угол параллелограмма равен b=180-120=60 градусов. это можно найти как сумма односторонних углов при пересечении параллельных прямых секущей.

 

Ответ: Углы параллелограмма 120 и 60 градусов.

image
(114k баллов)
Похожие задачи