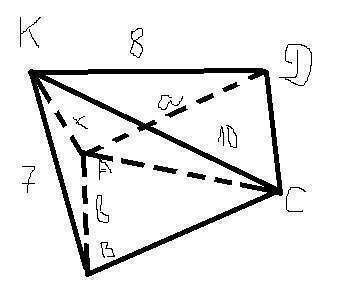
Дано: ABСD - прямоугольник.  . КВ=7 м, КD=8 м, КС=10 м.
. КВ=7 м, КD=8 м, КС=10 м.
Найти: АК.
Решение.
Пусть AD=а и AB=b - стороны прямоугольника.
Тогда по теореме Пифагора длина диагонали прямоугольника равна  м.
м.
Пусть АК=x м - длина искомого перпендикуляра. Тогда по теореме Пифагора
Получаем уравнение с длиной прямоугольника

Уравнение с шириной прямоугольника

Уравнение с диагональю прямоугольника

Сложим первое и второе уравнения. Получим



Вычтем из (*) уравнение (3). Получим


Ответ: