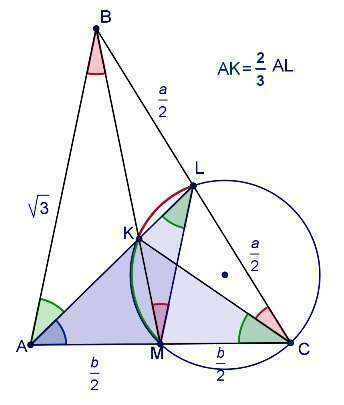
Чертеж к задаче во вложении.
1) L-середина ВС, М-середина АС, значит, ML - средняя линия треуг.АВС. Отсюда LM||AB, LM=0,5AB=(√3)/2
2) ∠BAL=∠ALM, ∠ABM=∠BML (накрест лежащие)
3) ∠LСK=∠KMN (опираются на одну и ту же дугу KL)
∠KLM=∠KCM (опираются на одну и ту же дугу KM)
4) Из всего этого следует подобие треугольников АСК и ALM по двум углам. Из подобия берем отношения сходственных сторон:

Обозначим для удобства ВС=а, АС=b.
По свойству точки пересечения медиан треугольника


Из равенства второго и третьего отношений получим

Теперь из первого и второго отношений:

Ответ: СК=1.