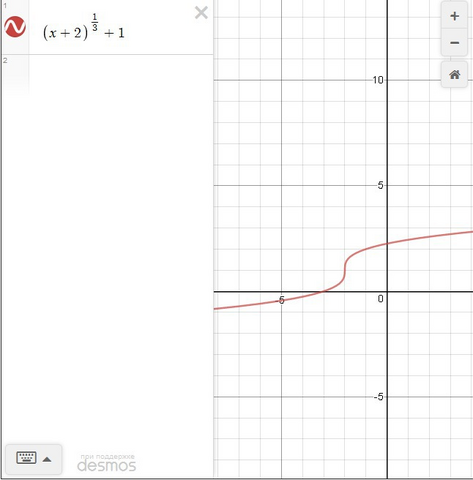
Построенный график ![y=\sqrt[3]{x+2}+1 y=\sqrt[3]{x+2}+1](https://tex.z-dn.net/?f=y%3D%5Csqrt%5B3%5D%7Bx%2B2%7D%2B1) смотри в приложении:
смотри в приложении:
1) Область определения функции: поскольку функция содержит кубический корень,  — любое число, то есть
— любое число, то есть 
2) Множество значений функции: последняя представляет собой кубическую параболу, следовательно, она определена на всём числовом промежутке, т. е.  — любое число, или
— любое число, или 
3) Чётность/нечётность: график данной функции симметричен относительно точки  . Значит функция нечётная;
. Значит функция нечётная;
4) Промежутки убывания возрастания: функция возрастает на протяжении всего графика;
5) Пересечения с осями координат: из графика чётко видно, что функция пересекает ось  в точке:
в точке: 
Точка пересечения оси  имеет дробную ординату. Чтобы найти её, приравняем значение аргумента к 0:
имеет дробную ординату. Чтобы найти её, приравняем значение аргумента к 0:
![y(0)=\sqrt[3]{0+2}+1,\\\\y(0)=\sqrt[3]2+1 y(0)=\sqrt[3]{0+2}+1,\\\\y(0)=\sqrt[3]2+1](https://tex.z-dn.net/?f=y%280%29%3D%5Csqrt%5B3%5D%7B0%2B2%7D%2B1%2C%5C%5C%5C%5Cy%280%29%3D%5Csqrt%5B3%5D2%2B1) ;
;
Получили точку пересечения графика функции оси
![OY:\ (\sqrt[3]2+1;\ 0) OY:\ (\sqrt[3]2+1;\ 0)](https://tex.z-dn.net/?f=OY%3A%5C+%28%5Csqrt%5B3%5D2%2B1%3B%5C+0%29) ;
;
6) Промежутки положительных и отрицательных значений функции:
 0" alt="y>0" align="absmiddle" class="latex-formula"> при
0" alt="y>0" align="absmiddle" class="latex-formula"> при  -3," alt="x>-3," align="absmiddle" class="latex-formula">
-3," alt="x>-3," align="absmiddle" class="latex-formula">
 при
при  ;
;
7) Наибольшее и наименьшее значения: для данной функции не существуют, поскольку она бесконечна на всё своём протяжении;
8) Ограничения: график функции неограничен;
9) Прерывность/непрерывность: функция непрерывна на всём своём протяжении.