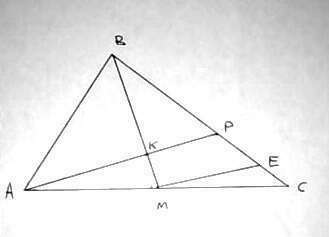
Проведем из точки M отрезок MЕ, параллельный AP, до пересечения со стороной ВС. Тогда по теореме Фалеса для угла АСВ и параллельных MЕ и AP отрезок MЕ будет делить на равные отрезки сторону угла СР, т.е. РЕ=ЕC.
Аналогично, по теореме Фалеса для угла СВА и параллельных MЕ и АР отрезок АР будет делить сторону ВЕ в отношении 7:3, т.е. ВР/PЕ = 7/3. Поэтому отношение ВР/ВС = 7/(7+3+3)=7/13.
Из условия задачи ВК/КМ=7/3, поэтому ВК/ВМ= 7/(7+3)=7/10.
Обзначим площадь треугольника BCM как S.
S=(1/2)*BM*BC*SinCBM.
Площадь треугольника ВКР S ВКР=(1/2)*BK*BP*SinCBM = (7/10)*(7/13)*S = (49/130)*S.
Площадь четырехугольника S KPCM = S - S ВКР = S - (49/130)*S = (1 - 49/130)*S = (81/130)*S.
Отношение площади треугольника ВКР к площади четырехугольника KPCM равно
((49/130)*S)/((81/130)*S) = 49/81.