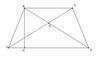
Пусть ABCD - равнобедренная трапеция с диагоналями BD и AC. Точка E - точка пересечения диагоналей. Треугольники EBC и AED подобны. Тогда
BE/ED = BC/AD. Следовательно, AD = BC*ED/BE. Отношение ED/BE по условию равно 5/2. Тогда AD = 8*5/2 = 20.
Для нахождения боковых сторон трапеции опустим высоту из вершины B: BH.
В треугольнике ABH катет AH равен (AD-BC)/2 = 6. Определим длину боковой стороны по теореме Пифагора:
AB^2 = BH^2 + AH^2
Тогда периметр ABCD = 8+12+10*2 = 40.