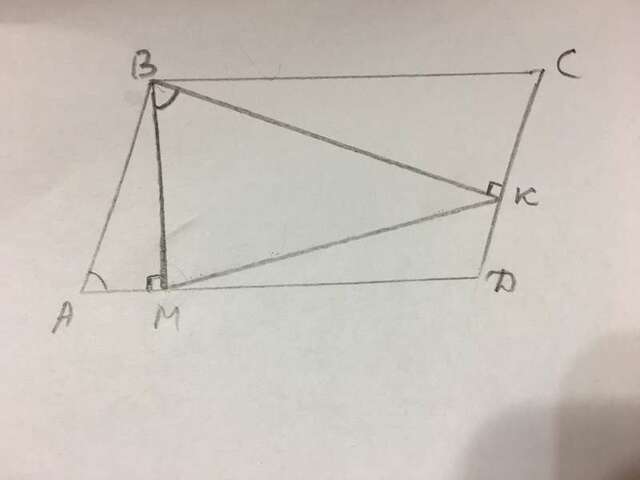
В параллелограмме АВСД ВМ и ВК - высоты. ВМ=56 см, ВК=60 см, КМ=52 см.
Углы между соответственно перпендикулярными прямыми равны.
ВМ⊥АД, ВК⊥СД, значит ∠МВК=∠ВАД.
В треугольнике ВМК по теореме косинусов cos(∠МВК)=(ВМ²+ВК²-КМ²)/(2·ВМ·ВК)=(56²+60²-52²)/(2·56·60)=0.6.
sin²α=1-cos²α.
sin²(∠ВАД)=1-0.6²=0.64,
sin(∠ВАД)=0.8.
Пусть АВ=х, АД=у.
Площадь параллелограмма: S=ху·sinα=0.8ху.
Также S=х·ВК=60х и S=у·ВМ=56у.
1) 0.8ху=60х,
у=60/0.8=75.
АД=75 см - это ответ.
2) 0.8ху=56у,
х=56/0.8=70.
АВ=70 см - это ответ.