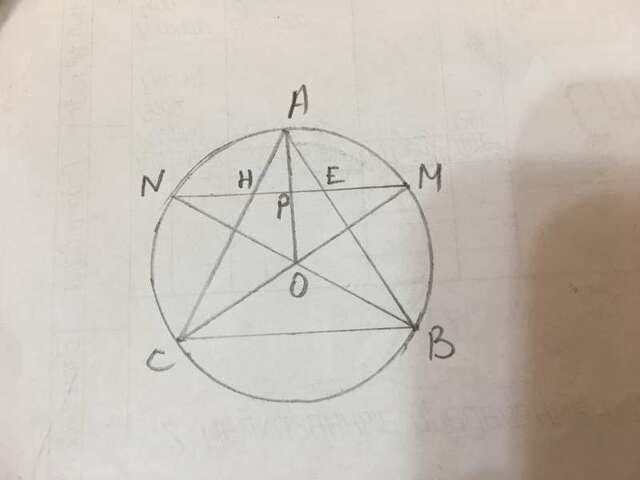
АВС - правильный треугольник со стороной а. АО - радиус описанной окружности. R=АО=а√3/3.
∠АОВ=∠ВОС=АОС=360/3=120°.
Так как точка М - середина дуги АВ, то ∠АОМ=∠АОВ/2=60°. Соответственно ∠АОN=60°, а ∠MON=120°.
Большая дуга MN равна 360-∠MON=360-120=240°.
Вписанный угол MAN опирается на дугу MN и равен её половине. ∠MAN=∩MN/2=240/2=120°.
Треугольники AMN и OMN равны, т.к. оба равнобедренные, у них общее основание и углы при вершинах равны, значит углы при основании тоже равны. Соответственно ΔOMN=ΔOBC, значит MN=BC=a.
В четырёхугольнике AMON стороны равны, значит он ромб, значит АР=РО. АР=R/2=а√3/6.
В правильном треугольнике АЕН АР - высота. Для правильного тр-ка h=a√3/2 (здесь а другая, только для формулы) ⇒ а=2h/√3.
ЕН=2·АР/√3=2·а√3/(6√3)=а/3 (здесь а - сторона тр-ка АВС. а=АВ).
MN=a, ЕН =а/3.
Исходя из симметрии построенного чертежа, ΔAMP=ΔANP, значит МЕ=NН.
МЕ=NН=(MN-ЕН)/2=(а-а/3)/2=а/3.
МЕ=ЕН=NН=а/3.
Доказано.