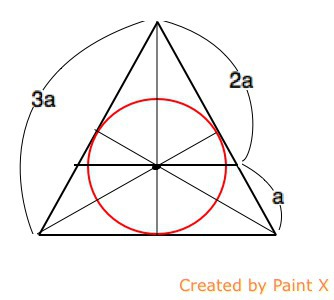
Окружность вписанная.
Центром вписанной в треугольник окружности является точка пересечения биссектрис углов треугольника.
Если точка пересечения биссектрис и точка пересечения медиан совпадают, то медианы треугольника являются и его биссектрисами.
Следовательно, данный треугольник - равносторонний.
Медианы треугольника пересекаются в одной точке. Точка пересечения медиан делит их в отношении 2:1, считая от вершины.
Прямая , параллельная стороне треугольника и равная 2 см, делит его на подобные треугольники с коэффициентом подобия 3:2 (вся медиана - 3 части, от вершины до точки пересечения медиан- 2 части, следовательно, и k=3:2)
Тогда таким же будет и отношение сторон всего треугольника к сторонам отсекаемого, т.е. к длине отрезка, на котором лежит центр окружности.
Обозначим сторону треугольника а.
а:2=3:2
2а=6
а=3 см
Периметр - сумма длин всех трех сторон треугольника.
Р=3•3=9 cм
----------
Если не прямая, на которой лежит центр окружности, равна 2 см, а сторона треугольника, тогда, естественно, периметр равен 6 см. Главное - определить, что треугольник равносторонний.