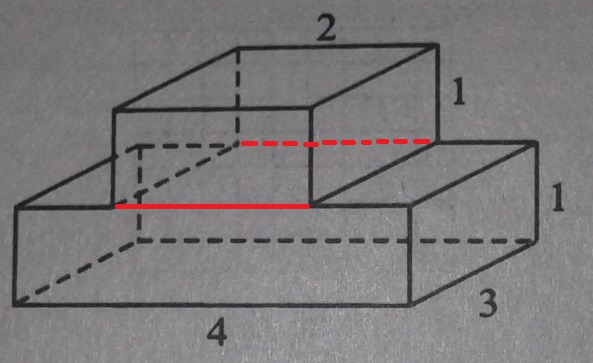
8. Площадь поверхности многогранника - это сумма площадей прямоугольников. Передняя и задняя части состоят из двух прямоугольников (см. рис.). Всего 12 прямоугольников. Из них "верх" и "низ" разные прямоугольники, остальные повторяются по 2 раза.
S = 2*3*1+2*3*1+2*3*1+2*2*1+2*4*1+2*3+4*3 = 6+6+6+4+8+6+12 = 48.
13.
1\;-\;He\;nogx.\\\cos x=\frac{\sqrt2}2\Rightarrow x=\pm\frac\pi4+2\pi n,\;n\in\mathbb{Z}\\\\b)\;\left[\frac{3\pi}2;\;\frac{5\pi}2\right]\\x_1=\frac{7\pi}4,\;x_2=\frac{9\pi}4" alt="a)\;3\sqrt2\sin\left(\frac\pi2+x\right)-2=2\cos^2x\\3\sqrt2\cos x-2=2\cos^2x\\2\cos^2x-3\sqrt2\cos x+2=0\\\cos x=t,\;\cos^x=t^2,\;-1\leq t\leq1\\2t^2-3\sqrt2t+2\\D=18-4\cdot2\cdot2=2\\t_{1,2}=\frac{3\sqrt2\pm\sqrt2}{4}\\t_1=\frac{\sqrt2}2\\t_2=2\sqrt2>1\;-\;He\;nogx.\\\cos x=\frac{\sqrt2}2\Rightarrow x=\pm\frac\pi4+2\pi n,\;n\in\mathbb{Z}\\\\b)\;\left[\frac{3\pi}2;\;\frac{5\pi}2\right]\\x_1=\frac{7\pi}4,\;x_2=\frac{9\pi}4" align="absmiddle" class="latex-formula">
