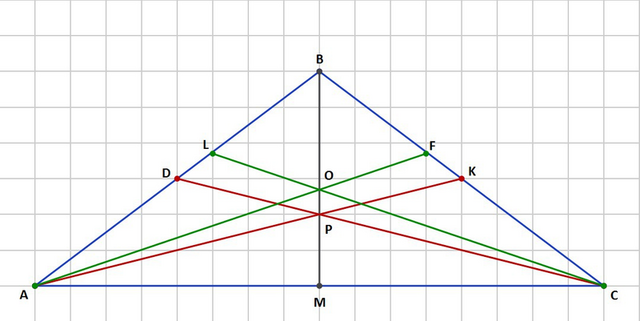
Для решения используются свойства медиан и биссектрис треугольников.
На рисунке показаны медианы (красным) и биссектрисы (зелёным). Точка пересечения медиан Р, точка пересечения биссектрис О. Необходимой найти расстояние ОР.
Из свойства равнобедренного треугольника медиана из угла, лежащего против основания, является биссектрисой и высотой. Следовательно треугольник АВМ - прямоугольный. По теореме Пифагора находим ВМ:
ВМ=√(АВ²-АМ²)
так как ВМ медиана, то АМ=МС или АМ=АС/2=16/2=8
ВМ=√(10²-8²)=√(100-64)=√36=6
Из свойств медианы: медианы треугольника пересекаются в одной точке и делятся точкой пересечения в отношении 2:1 считая от вершины, находим РМ:
РМ=ВМ/3=6/3=2.
Далее используем свойства биссектрисы: биссектриса треугольника делит стороны на отрезки, пропорциональные прилежащим сторонам. Для треугольника АВМ это свойство выглядит так:
ВО/ОМ=АВ/АМ
ВО=ВМ-ОМ=6-ОМ
подставляем вместо ВО
(6-ОМ)/ОМ=10/8
8(6-ОМ)=10ОМ
48-8ОМ=10ОМ
48=10ОМ+8ОМ
48=18ОМ
ОМ=48/18=8/3
ОР=ОМ-ОР=8/3-2=2/3
Ответ: расстояние между точкой пересечения медиан и точкой пересечения биссектрис равно 2/3.