Исследовать функцию и построить график. 
1) Находим область определения
Функция определена на всей числовой оси 
2) Точки пересечения графика функции с осями координат.
С осью Оу, т.е. х=0
у (0) = 0 - 3 * 0 + 2 = 2
С осью Ох , т.е. у =0

Очевидно, что х=1 является корнем уравнения, тогда разделим многочлен на (х-1), т.е. разложим на множители

Корни уравнения

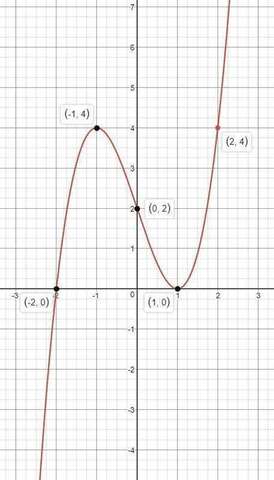
Функция имеет три точки пересечения с осями
(-2; 0) , (0; 2) , (1; 0)
3) Исследуем функцию на четность

Получаем что  и
и  , то функция не является четно, ни нечетной. Функция общего вида.
, то функция не является четно, ни нечетной. Функция общего вида.
4) Найдем асимптоты графика функции.
Функция не имеет точек разрыва, поэтому вертикальных асимптот нет.
Найдем наклонные асимптоты  , где
, где
![\[k=\mathop{\lim }\limits_{x\to \pm \infty } \frac{f\left(x\right)}{x} =\mathop{\lim }\limits_{x\to \pm \infty } \frac{x^{3} -3x+2 }{x} =x^{2} -3 + \frac{2}{x}=+\infty \] \[k=\mathop{\lim }\limits_{x\to \pm \infty } \frac{f\left(x\right)}{x} =\mathop{\lim }\limits_{x\to \pm \infty } \frac{x^{3} -3x+2 }{x} =x^{2} -3 + \frac{2}{x}=+\infty \]](https://tex.z-dn.net/?f=%5C%5Bk%3D%5Cmathop%7B%5Clim+%7D%5Climits_%7Bx%5Cto+%5Cpm+%5Cinfty+%7D+%5Cfrac%7Bf%5Cleft%28x%5Cright%29%7D%7Bx%7D+%3D%5Cmathop%7B%5Clim+%7D%5Climits_%7Bx%5Cto+%5Cpm+%5Cinfty+%7D+%5Cfrac%7Bx%5E%7B3%7D+-3x%2B2+%7D%7Bx%7D+%3Dx%5E%7B2%7D+-3+%2B++%5Cfrac%7B2%7D%7Bx%7D%3D%2B%5Cinfty+%5C%5D)
Наклонных асимптот тоже нет.
5) Найдем экстремум функции и интервалы возрастания, убывания. Для этого вычислим первую производную

Найдем критические точки, приравняв первую производную к нулю:

Эти точки разбивают область определения на три интервала. Находим знак производной  в каждом из интервалов
в каждом из интервалов
х x<-1 -1 -1<x<1 1 x>1
y' + 0 - 0 +
y возраст. max убыв. min возраст.
Точка (-1; 4) - точка максимума, точка (1; 0) - точка минимума.
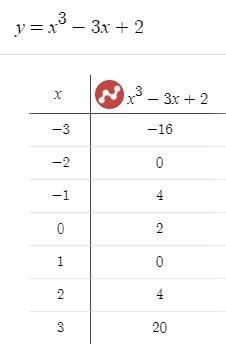
6) Строим график функции. Табличные данные и сам график, ниже