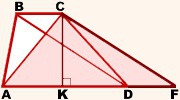
По условию АС=9 см; ВD=12 см;
m=7,5 см; m=(AD+BC)/2; AD+BC=7,5*2=15 см;
Проведем из вершины C на AD высоту CK.
Проведем через вершину С прямую, параллельную диагонали ВD. Пусть F - точка пересечения этой прямой с продолжением АD. ВСFD - параллелограмм, так как BC||DF и BD||CF.
СF = ВD = 12 см; DF=BC;
Площадь трапеции АВСD равна
S(ABCD)=m*CK;
Площадь треугольника АСF равна
S(ACF)=АF*CK/2=(AD+DF)*CK/2=m*CK;
Значит, S(ABCD)=S(ACF);
В треугольникеACF:
AF=AD+DF=AD+BC=15 см; АС=9 см; СF=12 см;
Зная три стороны площадь треугольника можно найти по формуле Герона.
р=(15+9+12):2=18 - полупериметр;
S(ACF)=√18*(18-15)*(18-12)*(18-9)=
√18*3*6*9=√9*6*6*9=9*6=54 см^2;
Но можно поступить проще.
Можно заметить, что треугольник со сторонами 9; 12 и 15 см - это прямоугольный треугольник (15^2=9^2+12^2). Поэтому площадь треугольника АСF равна половине произведения катетов.
S(ACF)=AC*CF/2=9*12/2=54 см^2;
Ответ: 54