ЗАДАЧА
Исследовать функцию
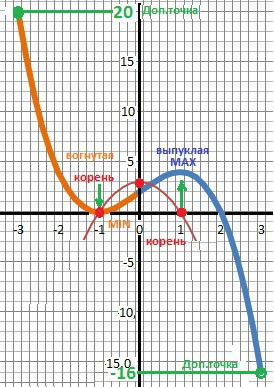
Y = - x³ + 3x + 2.
РЕШЕНИЕ
1. Область определения - Х = R или X =(-∞,+∞) - все действительные.
2. Точки пересечения с осью Х - х1 = х2 = -1 и х3 = 2
3 Корни производной равны 0.
Y' = - 3x² + 3 = 0 .Решение - х1 = - 1 и х2 = 1
4. Экстремумы.
Ymin = Y(0) = 0
Ymav = Y(1) = 2
5. Убывает при Х=(-∞,0]∪[1,+∞)
Возрастает при X=[-1,1]
6. Предельные значения
Lim(-∞) = +∞.
Lim(+∞) = -∞.
7. Дополнительные точки.
Y(-3) = +20
Y(+) = -16
Функция ни чётная ни нечётная.
8. Точка перегиба - вторая производная равна 0.
Y" = -6x = 0 при Х=0.
9. Вогнутая при X=(-∞,0]
Выпуклая при X=[0,+∞∞).
10. График в приложении.