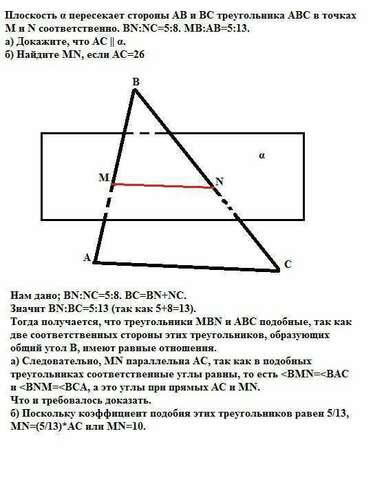
Нам дано; BN:NC=5:8. BC=BN+NC.
Значит BN:BC=5:13 (так как 5+8=13).
Тогда получается, что треугольники MBN и АВС подобные, так как
две соответственных стороны этих треугольников, образующих
общий угол В, имеют равные отношения.
а) Следовательно, MN параллельна АС, так как в подобных треугольниках соответственные углы равны, то есть Что и требовалось доказать.
б) Поскольку коэффициент подобия этих треугольников равен 5/13, MN=(5/13)*АС или MN=(5/13)*26=10.
Ответ: MN=10.