Решение задач по готовым рисункам. Тема "Трапеция"
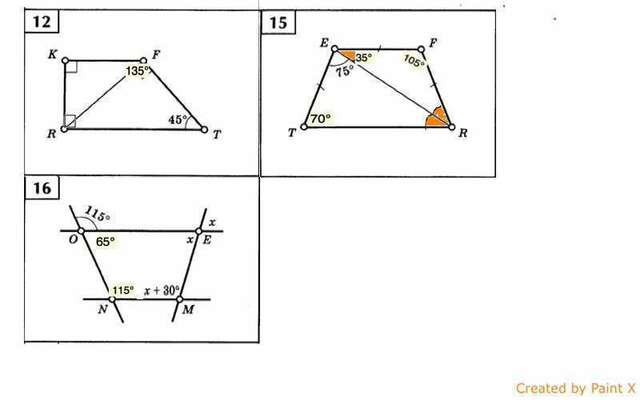
№12
Дана прямоугольная трапеция RKFT.
∠R=∠К=90º
Острый угол Т=45°, диагональ RF образует с большей боковой стороной угол =90°
Сумма углов трапеции, прилежащих к боковой стороне, равна 180° ( КF║RT, FT- секущая, сумма внутренних односторонних углов равна 180°)⇒
∠KFT=180°-45°=135°
----------------------
№15
Трапеция TEFR - равнобедренная. Меньшее основание равно боковым сторонам, угол TER=75º
В ∆ RFE стороны EF=FR, он равнобедренный,⇒ углы при его основании равны.
Пусть они равны х.
∠АЕК=∠ЕКЕ как накрестлежащие.
Тогда ∠FRT=2x
Поскольку трапеция равнобедренная, углы при основаниях равны, и ∠EТR=2х
Сумма углов трапеции, прилежащих к одной стороне, равна 180°
∠FET+∠ETR=180ª
2х+75°+х=180°⇒
х=35°
∠ETR=FRT=2•35º=70º
∠TEF=∠REF=75º+35ª=110º
-------------------
Задача №16
Поскольку тема - трапеции, две стороны которых параллельны, то ОЕ║NM
В четырехугольнике NOЕM угол, смежный с углом NOE=115º⇒
∠EON=180º-115º=65º
Тогда ∠ONM=18º-65º=115º
Угол ОЕМ равен вертикальному углу и равен х.
∠ОЕМ+∠EMN= 180° ( как внутренние односторонние углы при пересечении параллельных прямых секущей).
х+х+30°=180°
2х=150°
х=75°
∠ОЕМ=75°
∠EMN=75°+30°=105°