ДАНО
Уравнение параболы
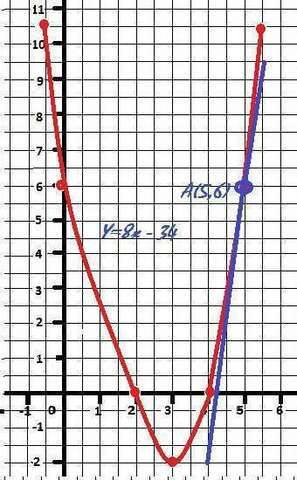
Y = 2x² - 12x +16 и точка касания А.
Находим производную функции.
Y' = 4x - 12
Уравнение прямой-касательной
Y = k*x + b.
Коэффициент k = Y'(5) = 20-12 = 8.
Находим ординату точки А.
У(5) = 2*25 -12*5 +16 = 50 - 60 + 16 = 6
Находим сдвиг прямой b из уравнения
У(5) = 8*5 + b = 6
b = 6-40 = -34
Уравнение касательной Y = 8x - 34 - ОТВЕТ
Графики прилагаются