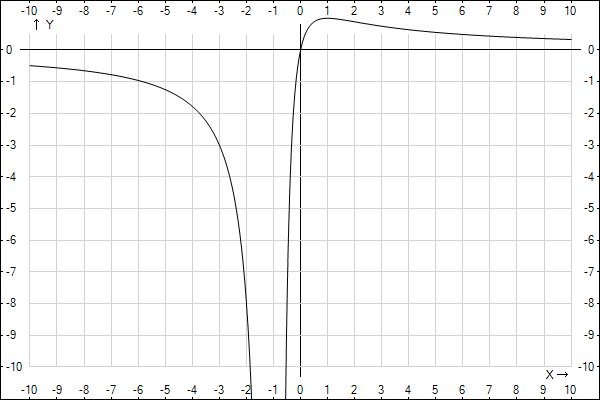
1.
2.
![y=\frac{4x}{(x+1)^2}, \\ y=\frac{4x}{x^2+2x+1}, \\ yx^2+2yx+y=4x, \\ yx^2+(2y-4)x+y=0, \\ yx^2+2(y-2)x+y=0, \\ D_{/4}=(y-2)^2-y\cdot y=y^2-4y+4-y^2=-4y+4, \\ D\geq0, -4y+4\geq0, \\ -4y\geq-4, \\ y\leq1, \\ E_y=(-\infty;1]; \\](https://tex.z-dn.net/?f=y%3D%5Cfrac%7B4x%7D%7B%28x%2B1%29%5E2%7D%2C+%5C%5C+y%3D%5Cfrac%7B4x%7D%7Bx%5E2%2B2x%2B1%7D%2C+%5C%5C+yx%5E2%2B2yx%2By%3D4x%2C+%5C%5C+yx%5E2%2B%282y-4%29x%2By%3D0%2C+%5C%5C+yx%5E2%2B2%28y-2%29x%2By%3D0%2C+%5C%5C+D_%7B%2F4%7D%3D%28y-2%29%5E2-y%5Ccdot+y%3Dy%5E2-4y%2B4-y%5E2%3D-4y%2B4%2C+%5C%5C+D%5Cgeq0%2C+-4y%2B4%5Cgeq0%2C+%5C%5C+-4y%5Cgeq-4%2C+%5C%5C+y%5Cleq1%2C+%5C%5C+E_y%3D%28-%5Cinfty%3B1%5D%3B+%5C%5C "y=\frac{4x}{(x+1)^2}, \\ y=\frac{4x}{x^2+2x+1}, \\ yx^2+2yx+y=4x, \\ yx^2+(2y-4)x+y=0, \\ yx^2+2(y-2)x+y=0, \\ D_{/4}=(y-2)^2-y\cdot y=y^2-4y+4-y^2=-4y+4, \\ D\geq0, -4y+4\geq0, \\ -4y\geq-4, \\ y\leq1, \\ E_y=(-\infty;1]; \\")
3.
4.
5.
_<0, \\ (x+1)^2\geq0, 4x^>_<0, x^>_<0, \\ x\in(0;+\infty), y>0, \\ x\in(-\infty;0), y<0; \\ " alt="\frac{4x}{(x+1)^2}^>_<0, \\ (x+1)^2\geq0, 4x^>_<0, x^>_<0, \\ x\in(0;+\infty), y>0, \\ x\in(-\infty;0), y<0; \\ " align="absmiddle" class="latex-formula">
6.
_<0, \frac{4-4x}{(x+1)^3}^>_<0, \\ -4(x-1)(x+1)^3^>_<0, \\ x\in(-\infty;-1), y'<0, y\searrow, \\ x\in(-1;1), y'>0, y\nearrow, \\ x\in(1;+\infty), y'<0, y\searrow; \\ " alt="y'=(\frac{4x}{(x+1)^2})'=\frac{4(x+1)^2-4x\cdot2(x+1)}{(x+1)^4}=\frac{(x+1)(4x+4-8x)}{(x+1)^4}=\frac{4-4x}{(x+1)^3}, \\ y'=0, \frac{4-4x}{(x+1)^3}=0, \\ (x+1)^3\neq0, x\neq-1, \\ 4-4x=0, -4x=-4, x=1; \\ y'^>_<0, \frac{4-4x}{(x+1)^3}^>_<0, \\ -4(x-1)(x+1)^3^>_<0, \\ x\in(-\infty;-1), y'<0, y\searrow, \\ x\in(-1;1), y'>0, y\nearrow, \\ x\in(1;+\infty), y'<0, y\searrow; \\ " align="absmiddle" class="latex-formula">
7.
