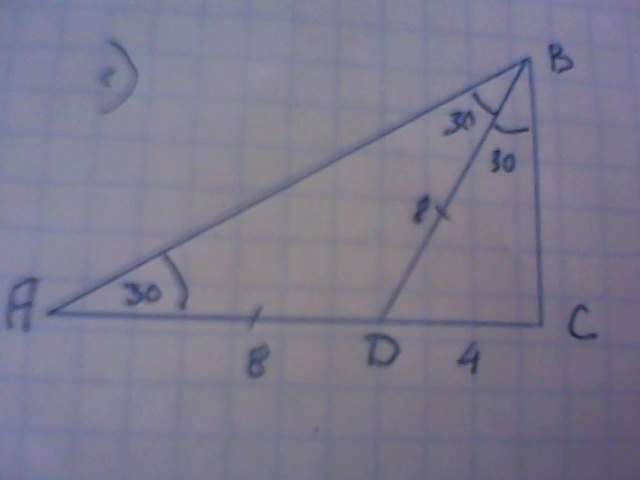
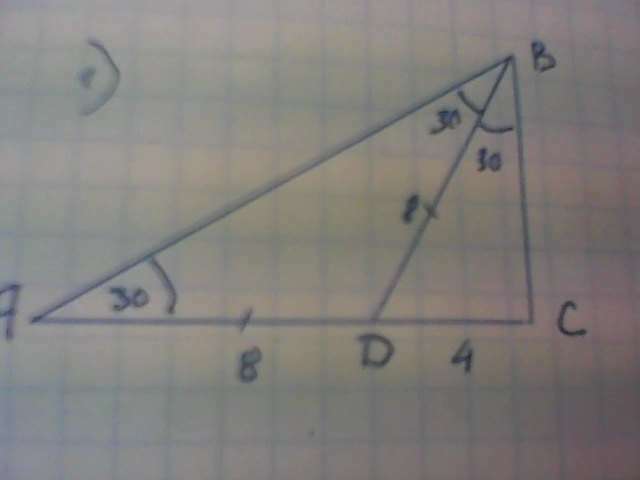
1) ΔАВС: ∠А=30°. значит ∠АВС=60°. ВD - биссектриса. ∠АВD=∠СВD=30°
ΔАВD - равнобедренный; АD=ВD=8.
ΔВСD.СD лежит против ∠СВD=30°. СD=0,5ВD=0,5·8=4.
ВС²=ВD²- СD²=64-16=48; ВС=√48=4√3.
АС=АD+СD=8+4=12.
Площадь ΔАВС=0,5·АС·ВС=0,5·12·4√3=24√3.
2) Пыстт=ь одна часть равна х. тогда АС=24х; АВ=25х
По свойству биссектрисы треугольника СD/ВD=АС/АВ, ВС=24+25=49.
ΔАВС. АВ² - АС² = ВС²,
625х² + 576х² = 2401,
49х² = 2401,
х²=49, х=7.
АВ=25х=25 · 7=175.
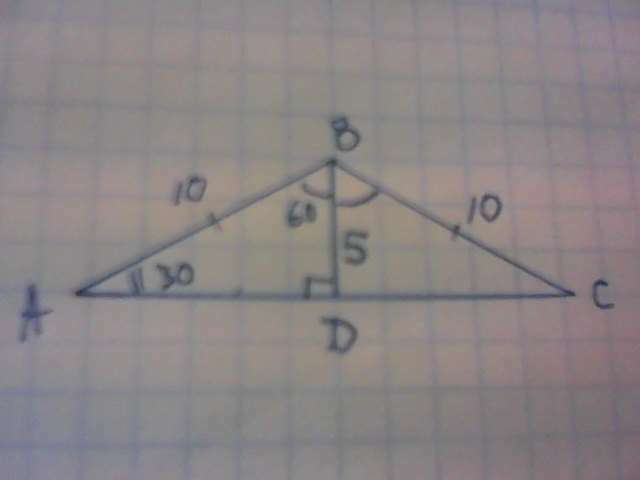
3) ΔАВD. ВD в равнобедренном треугольнике одновременно является биссектрисой, высотой и медианой. ∠АD90°.
∠ВАD=90-60=30°. ВD - катет лежащий против угла в 30° равен половине гипотенузы, ВD=10/2=5 м.