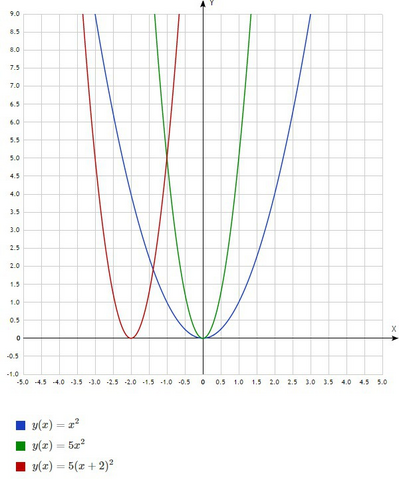
Чтобы было понятнее в качестве исходной функции рассмотрим функцию f(x)=x². Обычная парабола, симметричная относительно оси OY.
Для сжатия функции в 5 раз к оси ординат необходимо аргумент функции умножить на 5, тогда наша функция примет вид
f(5x)=5x² (зелёная парабола).
Прямая х=-2 параллельна оси ОY, поэтому необходимо выполнить сдвиг функции влево на два деления. Для этого необходимо к аргументу функции прибавить константу 2 (если прибавить -2, график сместится вправо). В нашем примере это будет выглядеть так
f(5(x+2))=5(x+2)² (красная парабола)
g(x)=f(5(x+2))
На мой взгляд как-то так.