Внутри двухгранного угла,равного120* данна точка М, удалённая от каждой из граней на...

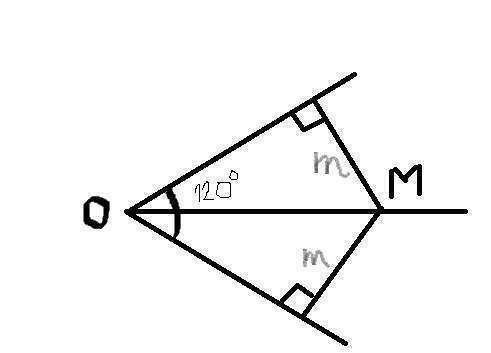
Если провести биссектрису через точку М и вершину этого двугранного, то получим два одинаковых прямоугольных треугольника. Угол в 120 градусов разделится пополам. Будет по 60 градусов. Расстоянием будет ОМ - гипотенуза этих треугольников. Катеты, противолежащие углу 60 градусов известны и равны m. Чтобы найти гипотенузу, надо катет, противолежащий углу в 60 градусов разделить на синус 60 градусов.

$OM=\frac{m}{\sin 60^0}=\frac{m}{\frac{\sqrt{3}}{2}}=\frac{2m}{\sqrt{3}}=\frac{2\sqrt{3}m}{3}$

Ответ: $\frac{2\sqrt{3}m}{3}$

Внутри двухгранного угла,равного120* данна точка М, удалённая от каждой из граней **...