Рассмотрим условие.
Сумма углов треугольника 180º.
∠А+∠В+∠С=180°
Если ∠AFC=128°, т.е. меньше угла В, то сумма углов ∆ АFС будет
∠С+0,5∠А+ ∠ AFC<142°=<u>меньше 180°.
Сделав рисунок, убедиться в этом несложно.
Итак, условие задачи должно быть таким:
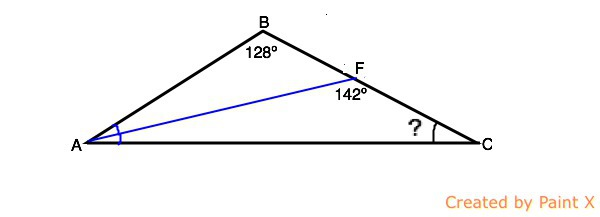
В треугольнике ABC проведена биссектриса AF, угол AFC=142°, угол ABC=128°.
Найдите угол ABC. Ответ дайте в градусах.
----------
Решение:
∠ВFA и ∠CFA смежные,⇒
∠ВFA=180°-142°=38°⇒
∠BAF=180°-128°-38°=14°
Половина ∠BAF=14º⇒∠BAC=28°
∠АСВ =180°-128°-28°=24°
Его можно найти и из ∆ AFC:
Угол AFB внешний при вершине F и равен сумме ∠FAC+∠FCA⇒
∠ACB=∠FCA=38°-14°=24°