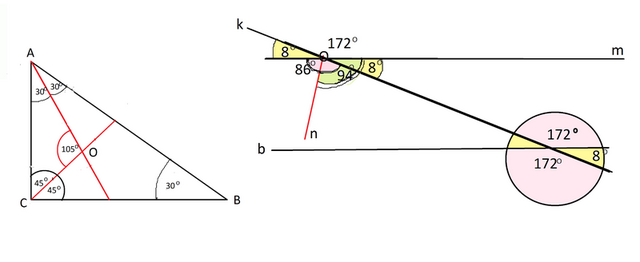
1)Сделаем рисунок. Обозначим вершины треугольника и точку пересечения биссектрис.
Рассмотрим треугольник АОС.
Сумма углов треугольника 180 градусов. поэтому угол САО равен 30 градусов.
Но этот угол - половина угла САВ. Отсюда угол САВ=60 градусов.
В треугольнике АВС угол АВС=30 градусов.
Меньший катет АС противолежит углу 30 градусов, поэтому гипотенуза АВ вдвое больше этого катета и равна 4 см.
-----------------------------------------
2)Обозначим точку пересечения секущей с m буквой О, а биссектрису большего угла буквой n.
Оn делит его на два равных угла, и половина его с острым углом составляет
94 градуса.
Отсюда вторая половина ( половина закрашенного розовым цветом угла) равна 180 - 94=86 градусов.
Весь тупой угол равен 86*2=172 градуса.
С острым углом он составляет развернутый угол и поэтому
острый угол равен 8 градусов.
Так как прямые m и n параллельны, секущая со второй прямой образует углы той же градусной меры.
Т.е. тупые углы равны 172 градуса, острые - 8 градусов.