Найдите производную: 1) f(x)=x-1/2 2) f(x)=(x^2+2x)/(x-1) Найдите первообрзаную: 1)...

$1) f^{'}(x) = 1\\ 2) f^{'}(x) = \frac{(2x+2)(x-1)-x(x+2)}{(x-1)^{2}} = \frac{(x+2)(x-2)}{(x-1)^{2}} = (\frac{x-2}{x-1})^{2}\\\\ 1)F(x) = \frac{x^{3}}{3}\\ 2)F(x)=\frac{5x^{5}}{5} = x^{5}\\$

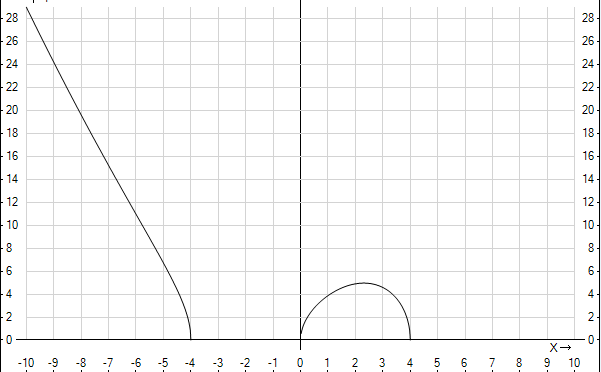
А с графиками:

1ый - парабола с ветвями вниз,сдвинутая на 4 единицы веерх

2ой - там просто подставляй точки и находи соответствующие y.Только точки надо братьс учетом области определения.По условию подкоренное выражение должно быть больше или равно нуля.Значит

$D(f) = (-\infty; 4] \cup [0; 4]$ ,

Второй график примерно такой должен быть(см.вложение)